Nikolaos Grigorios Kanellopoulos
| Field: | Computational Systems and Computer Science Applications |
| Rank: | Professor Emeritus |
| Government Gazette: | 1046/30-12-2009, τ. Γ' |
| Telephone: | +30 6932300003 |
| Email: | kane@ionio.gr |
| WWW: | https://orcid.org/0000-0001-5682-6395 |
| Office hours: | By arrangement |

Greece 2021 Committee Member:
Current Supervised Research:
Sonic Representations in Hyperspaces
Traperas, D., Floros, A. and Kanellopoulos, N. (2017), ‘Sonic representations in hyper-spaces: A creative approach’, Technoetic Arts: A Journal of Speculative Research, 15:2, pp. 221–28, DOI: 10.1386/tear.15.2.221_1
Description of the hyperspatial acoustic system
The various three-dimensional waveforms of sound are detected on two dimensional membranes, the eardrums. The perception of three-dimensional acoustic space is a process of combining this information and takes place mostly in the brain. In order to describe a hyperspatial acoustic system let us make the logical supposition that everything should correspond to one dimension above. The imprinting of the information of hyperspatial sound waves will occur not in two-dimensional membranes but in three-dimensional acoustic organs. The detection of the hyperspatial sound wave will be essentially achieved through a three-dimensional projection of it within the respectively three-dimensional hyperspatial eardrum. Part of the sound will be entrapped in this three-dimensional space and the corresponding organs will analyze and process it, being able to ‘traverse’ it in any direction, even backwards. The related information will be taken for processing to the higher processing organ in order to compose the hyperspatial information.
Description of an interactive installation art on acoustic hyperspace
Specific points in a given space are virtually designated to sources of sound. In the same way that written words can be imprinted on the surface of a piece of paper, so can sound be spatially imprinted in three dimensions. Then, the sensory organ for sound can ‘read’ it as it traces its course. Every point in space corresponds to a point in time of the sound, which no longer evolves in time since it is a spatial phenomenon. Visitors may approach and move away from the virtual sources and the distances that they keep from them are modified in proportion to their speed of movement. Every source creates its own acoustic space. Visitors’ perception of the sound emanated by a source depends on their distance from it and on the distance’s rate of change. Thus, they may perceive sound as evolving slowly, or quickly, or even stopping and, also, they can hear it correctly when moving away from a source that is when the distance is increasing or backwards when the distance is reducing.
Music track : Eagles-Hotel California (Don Felder, Don Henley, Glenn Frey)
VISUALISING THE HYPERSPHERE USING HINTON'S METHOD
(Traperas, Dimitrios and Kanellopoulos, Nikolaos (2018), ‘Visualizing the hypersphere using Hinton’s method’,
Technoetic Arts: A Journal of Speculative Research, 16:2)
3D SHPERE
4D SHPERE
CLICK ON THE COLORED CIRCLES FOR
INTERSECTION OF:
* 3D-SPHERE AND 2D-PLANE
* 4D-HYPERSPHERE AND 3D-SPACE
THE COLOR CORRESPONDS TO:
* THE AXIS OF THE 3D-SPHERE THAT IS PERPEDICULAR TO THE 2D-PLANE OR
* THE AXIS OF THE 4D-HYPERSPHERE THAT IS PERPEDICULAR TO THE 3D-SPACE
Johan Van Manen's 'Hypersphere'
Traperas, Dimitrios and Kanellopoulos, Nikolaos (2018), ‘An Interactive Art Application of a Proposed Fourth Spatial Dimension Cosmological Model’, International Conference on Digital Culture & AudioVisual Challenges, Ionian University, Corfu, 1-2 June
Occultist Johan Van Manen’s describes accurately a ‘fourth-dimensional globe’; i.e., a hypersphere:
[…] The fourth-dimensional globe can be better described. It was an ordinary three-dimensional globe, out of which on each side, beginning at its vertical circumference, bent tapering horns proceeded, which, with a circular bend, united their points above the globe from which they started. So three circles are formed, the lower one representing the initial globe, the upper one representing empty space, and the greater circle circumscribing the whole. If it be now understood that the upper circle [empty space] does not exist and the lower (small) circle is identical with the outer (large) circle, the impression [of the fourth-dimensional globe] will have been conveyed, at least to some extent […] (Van Manen, 1913: 58).
We propose that it is likely that Johan Van Manen envisioned not a hypersphere, but a projection to three-dimensional space of a hyper-solid that has some folds. It is this 3d visualization that he named (wrongly) “fourth-dimensional globe”. It is also interesting that Ouspensky does not agree with his interpretation of Johan Van Manen’s “fourth-dimensional globe” schema and comments that there might be a:
[…] possibility of constructing a certain pseudo-fourth dimension which, in actual fact, lies entirely in three dimensions. In my opinion the figure is full of motion. The whole figure seems to me moving, as though constantly arising in the meeting point of the sharp ends, spreading out from there and being re-absorbed there (Ouspensky, 2005: 134-35).
References
Van Manen, J. and Leadbeater, C.W. (ed) (1913). Some Occult Experiences. Adyar, Manras, India: Theosophical Publishing House. (described by Johan van Manen and annotated by C. W. Leadbeater)
Ouspensky, P.D. (2005). Τertium Οrganum: The Third Canon of Thought, a Key to the Enigmas of the World. New York: Cosimo Inc.
Interactive Art Application of a Proposed Fourth Spatial Dimension Cosmological Model: Investigating the Connection of the String Theory with Johan Van Manen's 'Hypersphere'
Traperas, Dimitrios and Kanellopoulos, Nikolaos (2018), ‘An Interactive Art Application of a Proposed Fourth Spatial Dimension Cosmological Model’, International Conference on Digital Culture & AudioVisual Challenges, Ionian University, Corfu, 1-2 June
Our proposed cosmological model of a 'double'-'closed' Universe is based on the following reasonings:
a) One of the models of our Universe, supported by Cosmology, is the ‘closed’ Universe, which is described by the three-dimensional hypersurface of a four-dimensional hypersphere. According to this theory, the evolution of this Universe is initially the expansion and then its contraction. (Guth, 2013 a & b)
b) While the General Theory of Relativity allows the Universe to start from a dimensionless point, as the ‘Big Bang’ theory argues, Quantum Theory claims that nothing can be compressed less than the Planck Length (1.616*10-33 cm). (Green, 2004: 337, 560-61) This incompatibility that exists at a microscopic level between those two Theories ceases to exist because of the Quantum Geometry of String Theory. According to this Theory, if we assume that for some reason the Universe begins to contract due to the gravitational force, then this continues contraction does not lead to a Universe ‘crush’ but to a Universe ‘bounce’. (Green, 2004: 342)
c) In the model of the Interrelated Notions of Distance (Green, 2004: 342), if the radius of a circular dimension is less than the Planck΄s Length and constantly decreases, based on Quantum Geometry, it does not differ from the natural processes where this dimension has a radius greater than the Planck’s Length and is constantly increasing.
d) The physical consequence of Quantum Geometry is that the physical properties of the Universe, based on the properties of its elemental components, are the same for a Universe whose circular dimension has a radius R with a Universe having a radius 1/R (where the value 1 means 1 time the Planck’s Length). (Green, 2004: 353)
e) Our Universe, on the basis of today’s data, stretches over 15 billion light years. However, we don’t know what happens beyond hat distance; i.e., whether the dimensions are unlimited or circular. If the Universe is circular, it can be subjected to the matching of the R and 1/R circular dimensions of String Theory. (Green, 2004: 354)
f) Johan Van Manen, at the end of his 'hypersphere' schema description, states that:
[…] If it be now understood that the upper circle does not exist and the lower (small) circle is identical with the outer (large) circle, the impression will have been conveyed, at least to some extent […]. (Ouspensky, 2005: 133)
That is, he suggests that the small ‘full’ sphere is the same as the ‘outer’ that encloses everything and essentially forms a solid.
We propose a new cosmological model of our Universe combining of all the above with emphasis on the model of the Interrelated Notions of Distance of Quantum Geometry (c above) with the statement of Johan Van Manen (f above). That is, its shape is similar with Johan Van Manen’s ‘folded’ hypersolid but the ‘outer’ sphere, which represents the ‘large’ Universe, has no fixed radius (R) and may be varied from infinity to zero. This variation affects the radius (1/R) of the smaller ‘full’ sphere, which, according to the Quantum Geometry Theory (d above), represents the parallel ‘small’ Universe, since there is an inverse ratio connecting the two radii (R and 1/R). So, the radius of the ‘full’ sphere conveys the value of the radius of the ‘empty’ sphere, since the sum of their diameters must be equal with the value of the ‘outer’ sphere’s diameter. When the two radii are equal to Planck’s Length (R=1/R=1), then the two ‘full’ spheres are equal and the ‘empty’ sphere is nullified and when the radius R of the ‘outer’ sphere increases, the radius 1/R of the ‘full’ sphere decreases . But, what happens while expanding the ‘outer’ sphere and the radius reaches (almost) an infinite value? Then, the ‘full’ sphere almost disappears, while the ‘empty’ sphere gets an (almost) infinite radius and occupies the innerspace of the ‘outer’ sphere.
If we accept that the ‘full’ and the ‘outer’ sphere are four-dimensional and the value of the radius of one of them is almost infinite then, according to our proposed model, the final result should be a three-dimensional hypersurface of a four-dimensional hypersphere that is constantly expanding and represents the ‘closed’ three-dimensional Universe we live in.
References
Green, B. (2003) (trans. Tsiantoulas, T.). The Elegant Universe: Superstrings, Hidden Dimensions, and the Quest for the Ultimate Theory. Athens: Oceanida.
Guth, A. (2013a). ‘Lecture 9: The Dynamics of Homogeneous Expansion, Part V’. MIT Open Courseware, MIT. Retrieved from https://ocw.mit.edu/courses/physics/8-286-the-early-universe-fall-2013/video-lectures/lecture-9-the-dynamics-of-homogeneous-expansion-part-v/
____ (2013b). ‘Lecture 11: Non-Euclidean Spaces: Closed Universes’. MIT Open Courseware, MIT. Retrieved from https://ocw.mit.edu/courses/physics/8-286-the-early-universe-fall-2013/video-lectures/lecture-11-non-euclidean-spaces-closed-universes/
Ouspensky, P.D. (2005). Τertium Οrganum: The Third Canon of Thought, a Key to the Enigmas of the World. New York: Cosimo Inc.
4D self-portrait
In the familiar 3D space, we can see and touch all sides of a square and its interior. Similarly, in the 4th spatial dimension, we must have visual and tactile access to the whole surface but also inside a cube. Picasso and the rest of the cubists came into contact with the 4th spatial dimension, mainly through discussions with Maurice Princet, and portrayed their subjects from many angles simultaneously in an attempt to reach the above dimension of the 4th dimension (Henderson, 2013). A later analogous approach is the photograph by Erwin Blumenfeld which we consider to best represent the 4-dimensional cubist view (Blumenfeld, 1999). We improved Blumenfeld’s idea employing audio-visual technics (Traperas, 2015).
Blumenfeld, E. (1999) Durch Tausendjährige Zeit. Erinnerungen. London, New York: Thames and Hudson.
Henderson, L. D. (2013) The Fourth Dimension and Non-Euclidean Geometry in Modern Art. Cambridge, Mass.: MIT Press.
Trapperas, D. (2015) Approaching 4D representations of 3D spaces. ΒΑ Thesis. Ionian University, School of Music & Audio-visual Arts, Department of Audio & Visual Arts.
Investigating the Connection Between Plato’s ‘Theory of Ideas’ and Hyperspaces
Traperas, D., Gounaropoulos, C. and Kanellopoulos, N.
TTT2020, Vienna, 26-28 November 2020
Our brain receives 2D information provided by our sense organs, processes this information and perceives 3D space that we live in. However, this perception does not exclude the existence of higher dimensional spaces, also known as ‘hyperspaces’. Neuroscientists in collaboration with mathematicians discovered recently that the neurons of the brain, while is processing 2D information, forms increasingly complex functional cliques and cavities, which correspond topologically to spaces of higher dimensions. Greek philosopher Plato suggested that supernatural entities, the ‘Ideas’, exist beyond our physical senses.
The authors propose that Plato’s world of ‘Ideas’ are related to the above mentioned higher dimensional geometrical brain structures.
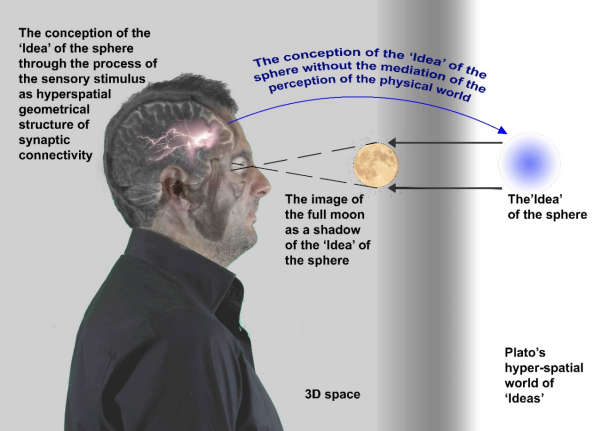
The cognitive procedure from the perception of the physical world to the conception of the world of ‘Ideas’. Courtesy of the authors (2020).
4D Hypersphere Perception via a Holographic Art Installation
Charilaos Gounaropoulos, Dimitrios Traperas, Nikolaos Kanellopoulos
DCAC’21, Corfu, 28-29 May 2021
Although the properties of fourth or higher dimensional hypersolids, as described by Topology, come as a result of the inductive method on Euclidean geometry in our familiar 2D and 3D space, we propose that there is a difficulty on the perception of higher dimensions, not as a result of the limited abilities of our sensory systems but on the deficient training of our brain in the specific topic. Audiovisual technology, in conjunction with Art, may provide the appropriate tools for developing application methods that could lead to the perception of the 4D hyperspace. As ‘TechnArtists’, based on a method for the perception of the 4D hypersphere, we developed an interactive holographic art installation as a training method for the visitor to perceive the hypersolid.
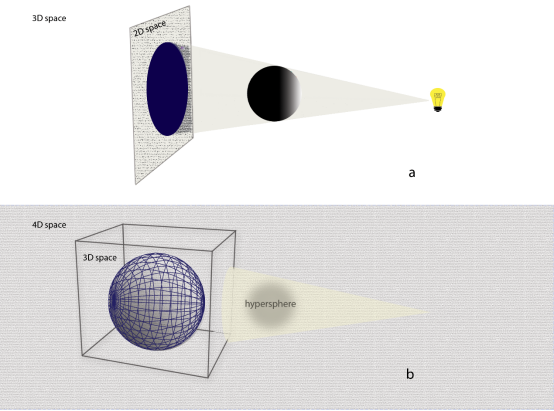
Figure 1a: 2D projection of a sphere. (© 2020 Traperas, Gounaropoulos and Kanellopoulos)
Figure 1b: 3D projection of a hypersphere. (© 2020 Traperas, Gounaropoulos and Kanellopoulos)

Figure 2: The Holographic Hypersphere installation as presented in Traperas’ exhibition. (© Dimitris Traperas, 2020).
Multimedia:
Studies/ Education:
-
1982:Ph.D: Electrical Engineering & Computer Science, University of Newcastle-upon-Tyne
-
1978:M.Sc(by research): Electrical Engineering & Computer Science, University of Newcastle-upon-Tyne
-
1976:B.Sc.(honours): Electrical Engineering & Computer Science, University of Newcastle-upon-Tyne
Research Interests:
-
Electronic Governing
-
Art and Culture
-
Environment
-
Computing Systems Architecture
-
Quality Reservation in Education, in Public Governing and in Industry
-
Computer Science Applications
Indicative Courses:
- Interaction using Physical Computing Interfaces
-
Introduction to Computer Science I
-
Introduction to Computer Science II
-
Business Dexterity and Art
-
Audiovisual Systems Design
-
Design - Organization of Audiovisual Projects
-
Audiovisual Installations Interaction Technologies
Academic Positions:
- 2020: Emeritus Professor, Department of Audio and Visual Arts
- 2017-8/2020: President, Department of Audio and Visual Arts
- 2016-2017: Vice President, Council of the Ionian University
- 2015-8/2020: Director of the Postgraduate Programme "Audiovisual Arts in the Digital Age"
- 2013-2017: Member of the Council, Ionian University
-
1/2010-8/2020: Professor, “Computing Systems and Computer Science Applications”, Audiovisual Department, Ionian University
-
11/2007-1/2010: Faculty Member, Department of Audio and Visual Arts
-
10/2007- 2012: President, Department of Audio and Visual Arts
-
1/2005-10/2007: Co-president, Computer Science Department, Ionian University
-
7/2004-10/2007: Associate Professor, Archives and Library Science Department, Ionian University
-
6/2003-7/2004: Faculty Member, Archives and Library Science Department, Ionian University
-
2000-2002: President, National School of Orchestral Art. Institution of High Education (Min. Culture)
-
1987-5/2003: Faculty Member, Department of Computer Mechanics & Informatics (Architecture and Hardware Sector), University of Patras
-
1980-1983: Professor's Assistant, University of Newcastle-upon-Tyne
Professional Experience:
-
1998-2010: Headmaster, Sector “Applications and Services of Stock Market” Researching Academical Institution of Computer Technology.
-
1996-2009: Athens Office Director, Researching Academical Institution of Computer Technology.
-
1996-2007: Scientific Director, Research Unit 4, “Computer Architecture & Communication Systems”, ΙΤΥ
-
1987-1996: Principal, Digital Systems Sector, ΙΤΥ
-
1986-1987: Principal, Digital Systems Laboratory, ΙΤΥ
-
1985-1986: Technical Director of Research and Development, SA
-
1983-1984: R&D Manager, Panorama Office Systems Ltd, UK
-
1978-1979: Researcher, International Computers Ltd Research Center, Manchester, UK
-
1977-1978: Researcher, “Digital Systems Laboratory” (DSL), Electrical Engineering & Computer Science Dept., University of Newcastle-upon-Tyne
Back



 Kanellopoulos Nikolaos Grigorios: Curriculum Vitae
Kanellopoulos Nikolaos Grigorios: Curriculum Vitae